Vamos a calcular la superficie del siguiente póligono que os mostramos en la fotografía.
El dibujo lo realizamos en el suelo con báldosas (cuadradas) , este nos servirá de cuadrícula.
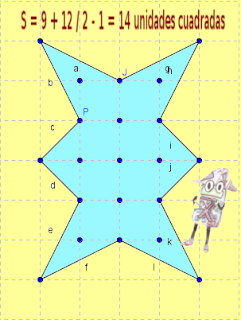
Otra imagen , del mismo polígono dibujada con el GeoGebra:
Vamos a calcular la superficie de este polígono , sirviéndonos de esta última imagen.
Para calcular la superficie de nuestro polígono , vamos a a aplicar una estrategia muy usada en las matemáticas y en la vida cotidiana: Divide y vencerás.
Vamos a descomponer , nuestro polígono en 4 triángulos isósceles y en un cuadrado.
Vamos a calcular la superficie de los triángulos isósceles.Vamos a suponer que las cuadrículas son cuadrados de dimensiones un número a unidades (cm,m,dm,...).
Sabemos que la Superficie de un triángulo es el producto de la base por la altura dividida por dos.Pero ,¿ cuánto vale la altura? , y la ¿base?
Cálculo de la base:
La base es fácil , si te fijas es la diagonal del cuadrado. Entonces aplicando el Teorema de Pitágoras:
d2 = a2 + a2 , donde d , va ser la base de nuestro triángulo.
Pero , ¿cómo calculamos la altura?.
Cálculo de la altura:
Vamos a tener que ingeniárnosla , vamos a calcular la altura del triángulo.
Lo primero que tenemos que hacer es observar que en el triángulo isósceles , contamos con dos triángulos rectángulos , lo cual ya nos permite usar el Teorema de Pitágoras.
Ahora ya estamos en condiciones de calcular la altura (h2) , fíjate :
Ahora calcularemos la superficie:
La superficie del triángulo es :
Pero claro tenemos 4 triángulos , entonces.
Ahora calcularemos la superficie del cuadrado , cuyo lado es dos veces la diagonal de la cuadrícula.
La superficie del cuadrado:
Evidentemente la superficie total será:
Luego la superficie de nuestro polígono es de 14 a2 unidades cuadradas.
Si a = 1 cm , entonces sería 14 cm2 ,si fuera a = 2 cm , entonces será 56 cm 2.
Bueno pues el Teorema de Pick , nos permite calcular la superficie de este polígono , de una manera muy sencilla. Sólo tenemos que contar .
Si te fijas en la malla de puntos , hay puntos que están en el interior del polígono (puntos interiores ,I ) y puntos que están en las aristas (puntos frontera ,B) . Una vez que los tenemos bien contados , tenemos que sustituir en una expresión algebraica , la Fórmula de Pick (S = I + B/2 - 1).
Finalmente tras sustituir en la fórmula tenemos:
También para calcular la superficie de nuestro polígono puedes usar un programa de dibujo vectorial como el Q CAD , aquí os muestro un pantallazo .
Vamos a suponer , que nuestra cuadrícula está compuesta por cuadrados de 10 cm de lado.
Con el Q CAD representamos , el polígono y con una de sus herramientas calculamos la superficie.
Una vez que , ya hemos visto diversas maneras para calcular la superficie de nuestro polígono, lo que tenemos que hacer es , medir las dimensiones de la baldosa (en nuestro caso una por ser un cuadrado) , y calcular la superficie , sustituyendo , a , por dicha medición en la expresión S = 14 a2, recordando que si expresamos la longitud del lado en cm , la superficie viene dada en cm2.
Aquí os dejamos unas fotos .Esta actividad fue realizada por los alumnos de 3º de Diversificación .Un especial recuerdo a Jony y a Fati.
Vamos a dibujar el polígono en el suelo.
Ya empezamos a trazar las aristas del polígono en el suelo.
Marcamos los puntos interiores , frontera y atacando,...
Finalmente , unas cuentitas.



















No hay comentarios:
Publicar un comentario